정렬은 크게 다섯가지로 나눌 수 있다: 버블정렬, 선택정렬, 병합정렬, 퀵정렬, 기수정렬(Radix Sort)
그 중 버블정렬과 선택정렬은 메모리 측면에서는 공간 복잡도 O(1)로 좋지만, 시간 복잡도는 O(n^2)로 비효율적이다.
반면 병합정렬과 퀵정렬은 시간 복잡도가 O(n logn)으로 조금 더 나은 성능을 보인다.
오늘은 배열을 정렬하는 문제를 통해 병합 정렬을 구현해보자.
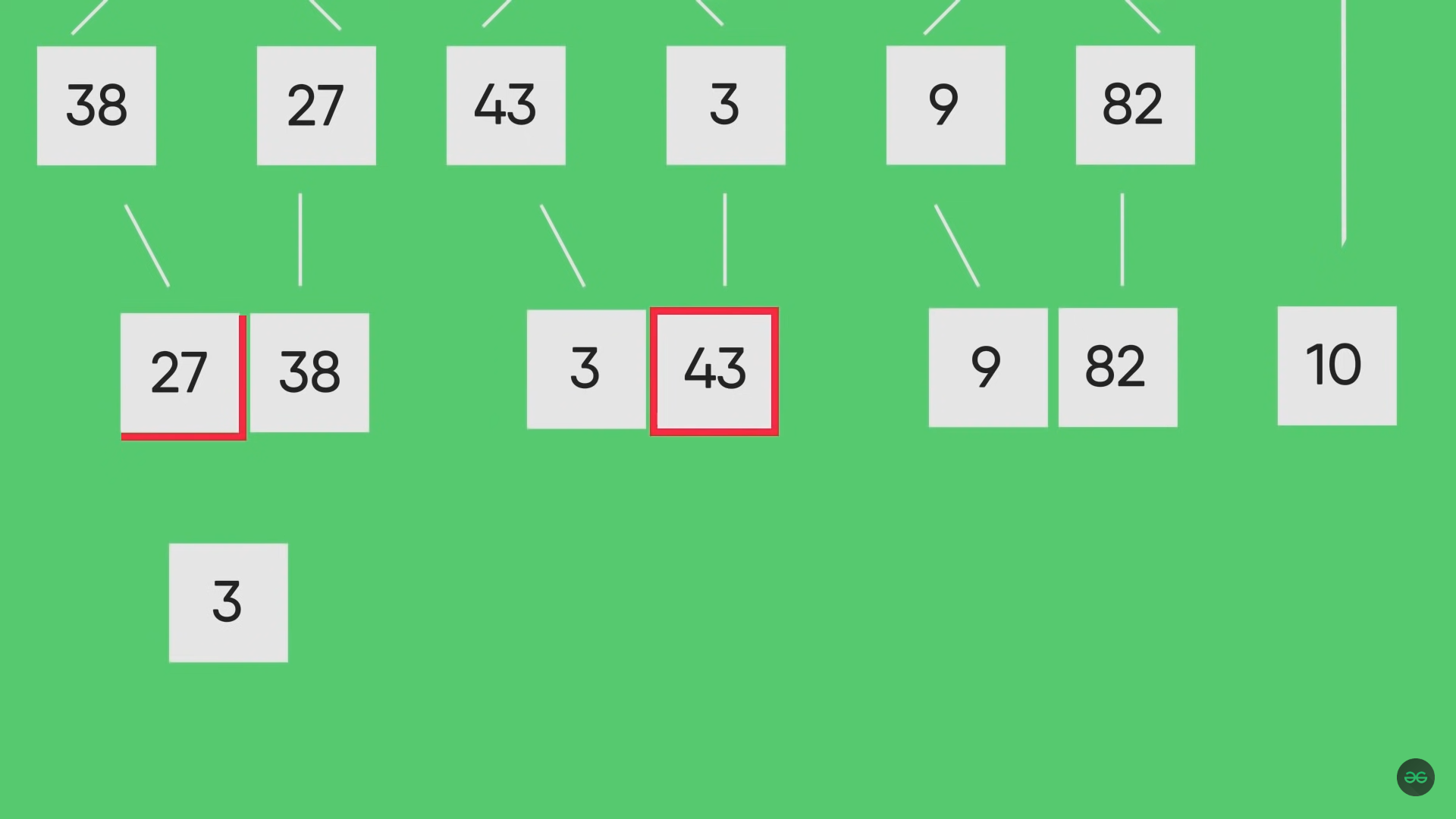
병합 정렬은 가운데를 기점으로 배열을 반 씩 나눠 정렬 후 병합하는 방법이다.
읽는 것 보다 보는게 이해하기 더 쉽다.
GeeksforGeeks의 예시 영상을 보자 : 링크
Python 코드
class Solution:
def sortArray(self, nums):
tmp = nums[:]
self.mergeSort(nums, tmp, 0, len(nums)-1)
return nums
def mergeSort(self, nums, tmp, left, right):
if left < right:
mid = int((left + right) / 2)
self.mergeSort(nums, tmp, left, mid)
self.mergeSort(nums, tmp, mid + 1, right)
self.merge(nums, tmp, left, mid, right)
def merge(self, nums, tmp, left, mid, right):
for i in range(left, right+1):
tmp[i] = nums[i]
helperLeft = left # 나눠진 배열 중 왼쪽 배열의 첫번째
helperRight = mid + 1 # 나눠진 배열 중 오른쪽 배열의 첫번째
current = left # 각 배열의 첫 번째 원소부터 비교
while helperLeft <= mid and helperRight <= right:
if tmp[helperLeft] < tmp[helperRight]:
nums[current] = tmp[helperLeft]
helperLeft += 1
else:
nums[current] = tmp[helperRight]
helperRight += 1
current += 1
remaining = mid - helperLeft
for i in range(0, remaining + 1):
nums[current + i] = tmp[helperLeft + i]CTCI 책(출처 참고)에 나온 Java 코드를 참고하여 Leetcode 문제에 맞게 작성된 코드입니다
실행 결과

병합 정렬은 O(n log(n))의 시간 복잡도를 가짐에도 다른 코드에 비해 그닥 런타임이 빠르지 않다.
그 이유는 예제와 같이 단순히 숫자를 정렬하는 경우에는 기수 정렬 (Radix Sort)가 더 빠르기 때문이다.
병합 정렬의 메모리는 어떻게 구현하느냐에 따라 달라진다
위 코드에서는 tmp 배열을 한 번만 할당하여 요소만 변경함으로써 더 적은 메모리를 사용하도록 했다.
다음 글에서는 같은 문제를 퀵정렬로 구현 후 성능을 비교해보자.
출처
- Cracking the Coding Interview - Chapter 10. Sorting and Searching
'개발 > 알고리즘 | 자료구조' 카테고리의 다른 글
| [알고리즘, Python] 아나그램(Anagram) 묶기 (0) | 2022.08.15 |
|---|---|
| [알고리즘, Python] Leetcode - 정렬된 두 배열을 합하는 문제(Merge Sorted Array) (0) | 2022.08.13 |
| [자료구조] 트리 (Tree) - 트리의 정의와 종류 (이진트리 등) (0) | 2022.08.10 |
| [알고리즘, Python] 정렬 2 - 퀵 정렬(Quick Sort) (0) | 2022.08.10 |
| [알고리즘, Python] 멱집합 (power set) / 부분집합 구하기 (0) | 2022.08.08 |